Can a drawing contain a kind of “absolute” truth? With exhaustive combinatorics, yes.
Consider this problem:

This really enjoyable 9-minute video takes us through the combinatorics for such circles. (Note that the video creator has chosen to use slightly different rules; he does not consider the one-point kissing circles to be valid; and that’s OK!)
Now consider graphs that connect points. From mathematician Arseny Khakhalin, here is a set of “all graphs with 3 nodes”. These are the only two possible topologies by which 3 things can be connected (not counting configurations in which a point is disconnected):

Here are all possible graphs of 4 nodes:
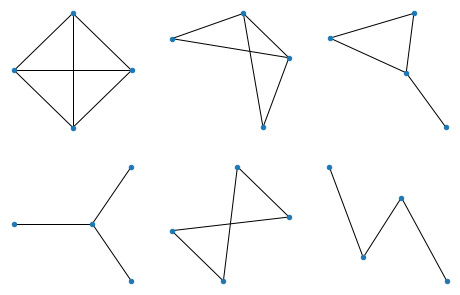
All graphs of 5 nodes:

All graphs of 6 nodes:

All graphs of 7 nodes:

In such depictions, generative rules are executed to their logical conclusion. The visual forms that result are no longer the arbitrary product of human imagination, but something more like a fundamental, irreducible property of the universe itself.
It may surprise you to learn that such rule-based images can also be considered artworks. “In 1974, American artist Sol LeWitt created one of his major works, a seminal piece on the themes of seriality and variation, the series entitled “Variations of Incomplete Open Cubes”. The work is a collection of 122 frame structures presented together with the corresponding diagrams arranged on a matrix. Each sculpture is the projection of a three-dimensional cube with some of the edges removed in a way that the structure stays three-dimensional and the edges stay all connected. The minimum number of edges kept is three and the maximum is eleven.” [Source]. Lewitt’s artwork depicts all possible combinations of cube-edges that meet these conditions. There are no other possibilities: all possibilities are included and none are missing.

Here’s a simpler and more idiosyncratic example. Lewitt’s Geometric Figures Within Geometric Figures (1976), which shows all possible pairings of six basic shapes, hints at how conducting such studies can be a tool for design exploration, while retaining the power of a statement of mathematical fact.

Here’s a more recent example, which illustrates the risk of combinatoric explosion. Arc Forms by Christopher Carlson (2009) shows all possible combinations of semicircles joined at 3 connection points evenly distributed along a vertical line. (He includes the cases in which they aren’t there, too.)

But be careful. Change the number of connection points for such arcs, and the possibility space balloons dramatically:
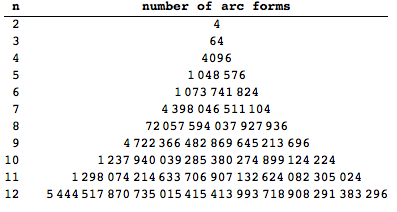
Clearly, you can choose to design a visual system for which it is practical to enumerate all possible combinations — or you may design one for which it isn’t. One can impose additional criteria to narrow the space once more. In curating the rules by which such gargantuan spaces are filtered and culled, the voice of the ‘artist’ reemerges, producing an idiosyncratic design language through sub-selection:

All of the systems described on this page are:
instances of “minimum inventory/maximum diversity” systems, a term coined by Peter Pearce in his book, Structure in Nature Is a Strategy for Design (MIT Press, 1978). A minimum inventory/maximum diversity system is a kit of modular parts and rules of assembly that gives you maximal design bang for your design-component buck. It’s a system that achieves a wide variety of effects from a small variety of parts. Nature excels at this game: every one of the many millions of natural proteins is assembled from an inventory of just 20 amino acids. Snowflakes are all just arrangements of the humble water molecule, H2O. [Source]
In other words: using very simple rules/constraints, we can get profound and surprising diversity. Here are a few more such systems:
Michael Fogleman, SQUARES IN A SQUARE (2021). Fogleman asks: “How many ways can you chop up an NxN square into integer-sized squares? 1, 1, 2, 6, 40, 472, 10668. Here is N=5 (but rotation-invariant)”: 
Michael Fogleman, MOWING A LAWN (2021): The number of ways to mow a square of size N (N=7):

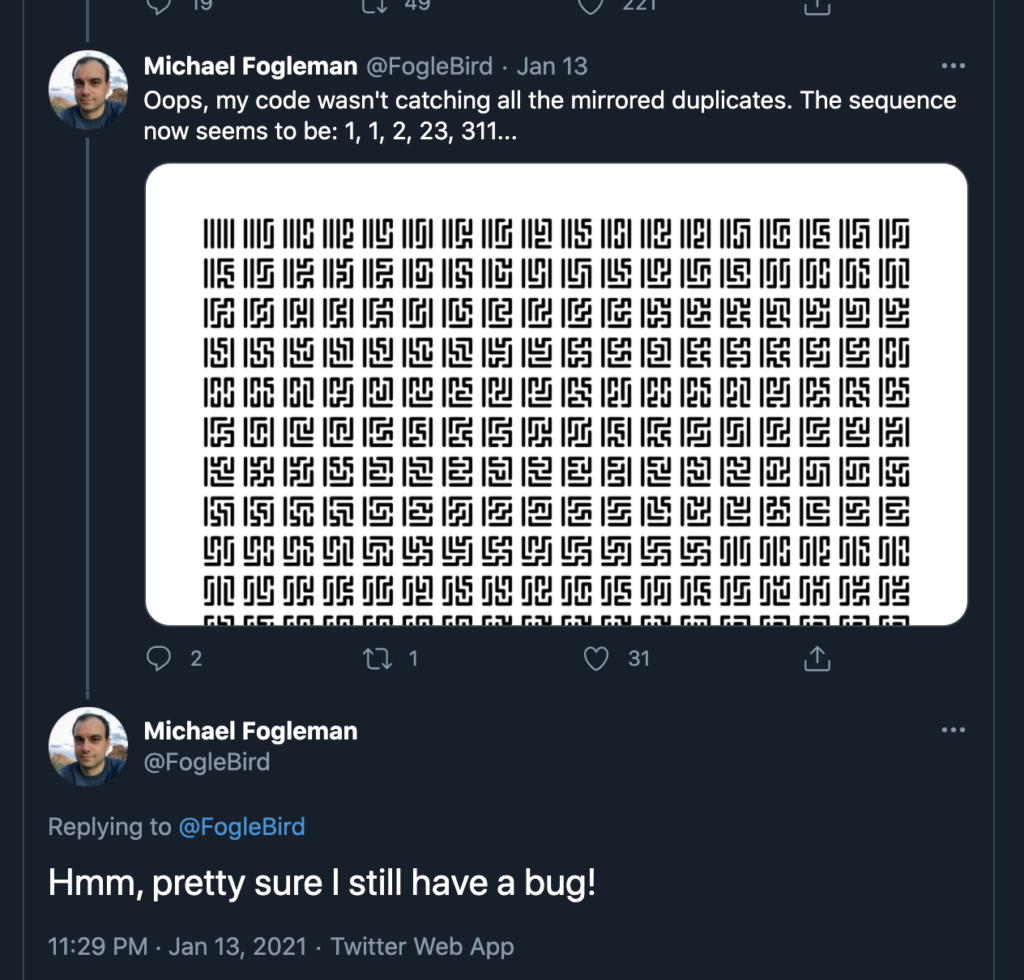
By the way, here’s a case in which Fogleman is failing in public. He thought his algorithm for computing combinatorics was correct… and then concedes he had a bug. It can be tricky to verify that these systems are correct, even for experts!
One last one. Here’s Michael Joaquin Grey’s Erosion Blocks (c.1990), a sculpture which shows progressive combinatoric removals of the sides of a rectangular prism, leaving (at the end) the potato-like Philosopher’s Stone. These 43 blocks illustrate the following truth: they are the only possible ways of removing 0,1,2,3,4,5, and 6 sides from a rectangular prism with a square cross-section.

This stuff is difficult for me. What’s the easiest place to start?
Try asking yourself a question about simple shapes that has a discrete, countable answer. Start with small numbers of things. Here’s an example, in the form of a question: “How many logically distinct ways can I arrange 1 hexagon? 2 hexagons? 3 hexagons? 4 hexagons?” (These are called ‘polyhexes‘ by the way). (Also: “Logically distinct” is different from “visually distinct”; for example two visually-different configurations might be considered logically similar if you can obtain one from the other by rotating it or flipping it.) So, coming up with such a question and showing all of the tetrahexes would be a perfectly legitimate response to the homework prompt. But note: the homework is much more concerned with your ability to come up with a question like that, than to actually correctly work out all of the permutations!
